スタックとヒープの違い
スタックとヒープ
スタックは順序付きリストで、リスト項目の挿入と削除は、上。この理由により、スタックはLIFO(Last in First Out)データ構造と見なされます。ヒープは、ツリーに基づいた特別なデータ構造であり、ヒーププロパティと呼ばれる特別なプロパティを満たします。また、ヒープは完全なツリーです。つまり、ツリーの葉の間に隙間がないことを意味します。 e。完全なツリーでは、ツリーに新しいレベルを追加する前にすべてのレベルが塗りつぶされ、与えられたレベルのノードは左から右に塗りつぶされます。
スタックとは何ですか?前述したように、スタックは、要素がトップと呼ばれる一端からのみ追加されて削除されるデータ構造です。スタックでは、pushとpopという2つの基本操作のみが可能です。プッシュ操作では、新しい要素がスタックの最上部に追加されます。 pop操作は、要素をスタックの先頭から削除します。スタックがすでに満杯の場合、プッシュ操作が実行されると、スタックオーバーフローとみなされます。既に空のスタックでポップ操作が実行された場合、スタックアンダーフローと見なされます。スタック上で実行できる操作の数が少ないため、制限されたデータ構造と見なされます。さらに、pushおよびpop操作が定義されている方法によれば、最後にスタックに追加された要素が最初にスタックから出ることは明らかです。したがって、スタックはLIFOデータ構造と見なされます。
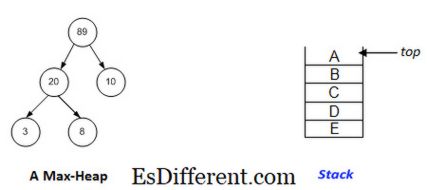
前述のように、ヒープはヒーププロパティを満たす完全なツリーです。 Heapプロパティは、yがxの子ノードである場合、ノードxに格納された値はノードyに格納された値以上でなければならないと述べている(すなわち、値(x)≧値(y))。このプロパティは、最大の値を持つノードが常にルートに配置されることを意味します。このプロパティを使用して構築されたヒープは、最大ヒープと呼ばれます。ヒーププロパティには、これとは逆の別のバリエーションがあります。 (すなわち、値(x)≦値(y))。これは、最小の値を持つノードが常にルートに配置されることを意味し、したがって、最小ヒープと呼ばれます。ヒープには、最小値(最小ヒープ数)または最大値(最大ヒープ数)、最小値(最小ヒープ数)または最大値(最大ヒープ数)の削除、最大値-heaps)キーまたは減少(min-heapsキー)キーなど
スタックとヒープの主な違いは、スタックが線形データ構造である一方、ヒープは非線形データ構造であることです。 Stackは、LIFOプロパティの後に続く順序リストで、ヒープはヒーププロパティの後に続く完全なツリーです。さらに、スタックは、限られた数の操作をプッシュおよびポップとしてサポートする制限付きのデータ構造ですが、ヒープは、最小値または最大値の検索および削除、キーの増減、マージなどの幅広い操作をサポートします。


