パワー・シリーズとテイラー・シリーズの違い
Power SeriesとTaylor Series
数学では、実際のシーケンスは、 。正式には、自然数の集合から実数の集合までの関数です。 999 n 999が配列のn 999番目の用語である場合、本発明者らは、配列を999,999,999 999、…、999、…、999、例えば、シーケンス1、1 / 2,1 / 3、…、999 / 999,999 …を考える。それは{1 / n}と表すことができます。 シーケンスを使って系列を定義することは可能です。系列とは、系列の項の和です。したがって、各配列について、関連する配列があり、逆もまた同様である。考慮中のシーケンスが{a 999} である場合、そのシーケンスによって形成される系列は、 <!したがって、上記の例では、関連する系列は、1 + 999/999 + 9999/9993である + … + 9999/9999 + …。 名前が示すように、力級数は特殊型のシリーズであり、数値解析や関連する数学的モデリングに広く使用されています。テイラーシリーズは、よく知られている機能を表現するための代替的で操作しやすい方法を提供する特殊なパワーシリーズです。 <! - > - > Power seriesとは何ですか? 力級数は、 <! (おそらく) c を中心としたある間隔で収束している - 1 - > 。係数999は、実数または複素数であってもよく、999×999から独立している。私。 e。 はダミー変数です。例えば、各999および999 = 999に対して999 n 999 = 1を設定することによって、べき級数1 + x + x 2 999 + … + x 999 n + …が得られる。 xε(-1,1)のとき、このべき級数は1 /(1-x)に収束することは容易に分かります。 <!べき級数は、 999 = 999cで収束する。力級数が収束する x
の他の値は、常にcを中心とする開放区間の形をとる。 | R を満たす各999×999に対して、 R >、累乗系列は収束し、| xc |> R
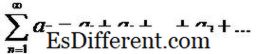
x については、べき級数は発散的である。この値 R は、べき級数の輻輳半径と呼ばれます( R は実数または正の無限大を取ることができます)。 <! - > - 次のルールを使用して、べき級数を加算、減算、掛け算、および除算することができます。 2つの力級数を考えてみましょう: 。次に、
そして
によって与えられるべき級数は、 - 9 - >は、約999の関数のテイラー級数展開と呼ばれている。 999(999)(999)(999)(999)は、999番目の誘導体を示し、 c
)。数値解析では、この無限拡張の項の有限数を、系列が元の関数に収束する点での値の計算に使用します。各x∈(a、b(999)、b(999))に対して、関数f 999(999×999) )、テイラー級数999(999×999)は関数999(999×999)に収束する。例えば、テイラー展開1 + x + x 999 2 999 + … + x 999 n 999 + …が収束するので、1 /(1-x)は(-1,1) 999×999のテイラー級数が999×999に収束するので、999×999はその区間の関数に対応し、各実数
xに対してとなる。
PowerシリーズとTaylorシリーズの違いは何ですか? 1。 Taylorシリーズは、いくつかのオープンな間隔で無限に微分可能な関数に対してのみ定義されるべき級数の特別なクラスです。 2。テイラー級数は特別な形 をとりますが、級数は形



