データ構造のツリーとグラフの違い|ツリーとデータ構造のグラフ
ツリーとデータ構造のグラフ
ツリーとグラフは、複雑なコンピュータの問題を解決するために使用される非線形データ構造です。データ構造内のツリーとグラフの違いがわかっていれば便利です。両方のデータ構造は、数学的形式のデータ項目を表す。この記事の主な目的は、非線形データ構造の重要性を強調することです。また、これら2つのデータ構造の主な違いも含まれています。
データ構造内のツリーとは何ですか?ツリーは、すべてのデータ項目が何らかのソートされた順序で配列された非線形データ構造である。ツリーは、データ項目の有限集合を定義する。各データ項目はノードと呼ばれます。ルートノードとも呼ばれる特殊な親ノードがあります。他のすべてのノードは、子ノードまたは子子ノードです。ツリーの主な目的は、異なるデータ項目間の階層関係を表現することです。通常木は上方向に成長するが、データ構造ツリーは下方向に成長する。ツリーに添付されたすべてのサブノードは、さまざまなレベルに分割されています。バイナリツリーは、非線形データ構造の最も一般的な例です。バイナリツリーの最大次数は2です。つまり、親ノードごとに最大2つのノードを接続できます。

グラフは、さまざまなコンピュータの問題を解決するために使用される一般的な非線形データ構造です。彼らは様々なゲームやパズルをデザインするために使用されます。グラフは多くのカテゴリに分類できます。これらは次のとおりです。
<! Directed Graph:有向グラフでは、各エッジは、順序付けられた頂点のペアによって定義されます。
無指向グラフ:無向グラフでは、各エッジは、順序付けされていない一対の頂点によって定義されます。 • 接続グラフ:
接続パスには、すべての頂点から他の頂点までのパス。 • 非連結グラフ:
非連結グラフでは、頂点から他の頂点までのパスが存在しません。 • 加重グラフ:
加重グラフでは、ある加重がエッジに付いています。 •単純グラフ または
マルチグラフ データ構造におけるツリーとグラフの類似点 •ツリーとグラフは両方とも、複雑なコンピュータを解決するために使用される非線形データ構造です問題。
•どちらのデータ構造も、親ノードと複数のサブノードを使用します。 データ構造のツリーとグラフの違いは何ですか? •ツリーはグラフの特殊ケースとみなされます。これは最小接続グラフとも呼ばれます。 •すべてのツリーはグラフとして考えることができますが、すべてのグラフをツリーとみなすことはできません。
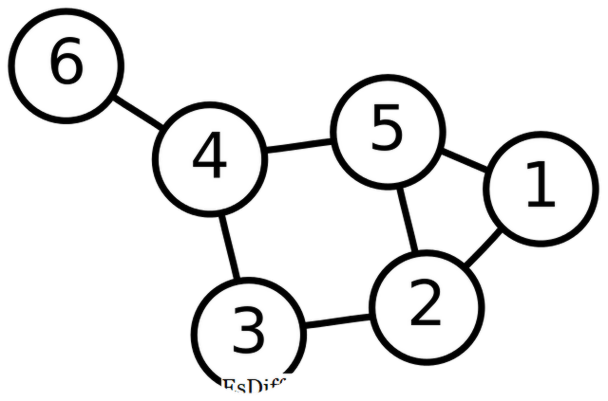
•セルフループと回路は、グラフの場合のようにツリー内で使用できません。
•ツリーの設計には、親ノードとさまざまなサブノードが必要です。グラフを設計するには、頂点とエッジが必要です。エッジは一対の頂点です。上記の議論は、ツリーおよびグラフが、様々な複雑な問題を解決するために使用される最も一般的なデータ構造であると結論づけている。グラフは、コンピュータ設計、物理的構造およびエンジニアリング科学で使用される、より一般的なデータ構造です。ほとんどのパズルは、グラフのデータ構造の助けを借りて設計されています。最短距離の問題は、最も一般的に使用されるデータ構造です。この問題では、2つの頂点間の最短距離を計算する必要があります。
今後の展望:




