差平行四辺形と菱形の違い:平行四辺形と菱形
平行四辺形と菱形
平行四辺形と菱形は四辺形です。これらの図形の幾何学は何千年もの間人類に知られていました。主題は、ギリシアの数学者ユークリッドによって書かれた本の「要素」で明示的に扱われている。
平行四辺形
平行四辺形は、4つの辺を有する幾何学的図形であり、互いに反対の辺が平行であると定義することができる。より正確には、2組の平行な辺を有する四辺形である。この並列性は、平行四辺形に多くの幾何学的特性を与える。

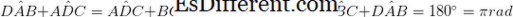
四角形は、幾何学的特性が次のような場合に平行四辺形です。
•2対の対向する辺の長さは等しい。 (AB = DC、AD = BC)
•2対の対向する角度の大きさは等しい。 (
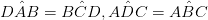
•隣接する角度が補助的な場合
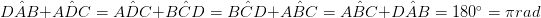
•互いに対向する一対の辺が平行で長さが同じです。 (AB = DC&AB‖DC)
<! (AO = OC、BO = OD)•各対角線は、四辺形を2つの合同三角形に分割する。 (ΔADB≡ΔBCD、ΔABC≡ΔADC)さらに、辺の二乗の和は、対角線の二乗の和に等しい。これは時には平行四辺形法
と呼ばれ、物理学と工学に幅広く応用されています。 (AB 999 + BC 999 + CD 999 + DA 999 = AC 999 + BD 999) 2つの四辺形が平行四辺形であることが証明されると、上記の特性のそれぞれを特性として使用することができる。平行四辺形の面積は、片側の長さと反対側の高さとの積によって計算することができる。したがって、平行四辺形の面積は、平行四辺形の面積=底辺×高さ= AB×hと表すことができる。平行四辺形の面積は、個々の平行四辺形の形状とは無関係である。ベースの長さと垂直高さにのみ依存します。平行四辺形の辺を2つのベクトルで表すことができる場合には、隣接する2つのベクトルのベクトル積(外積)の大きさによって面積を求めることができる。辺ABと辺ABがそれぞれベクトル(
と )で表される場合、平行四辺形の面積は によって与えられ、ここでαは との間の角度である>。 平行四辺形のいくつかの高度な特性がある。 •平行四辺形の面積は、対角線のいずれかによって作成された三角形の面積の2倍です。 •平行四辺形の面積は、中点を通る線の半分に分割されます。 •非縮退アフィン変換は、平行四辺形を別の平行四辺形に変換します。•平行四辺形は、次数2の回転対称性を持ちます。•平行四辺形の任意の内部点から辺までの距離の合計は、ポイントの位置 菱形 すべての辺の長さが等しい四角形は、菱形として知られています。 正四角形 とも呼ばれます。トランプカードに似た菱形をしていると考えられます。 菱形も平行四辺形の特殊なケースです。それは、4辺がすべて等しい平行四辺形と考えることができます。また、平行四辺形のプロパティに加えて、以下の特殊なプロパティがあります。 •菱形の対角線は互いに直角に二等分する。対角線は垂直です。 •対角線は2つの対向する内角を二等分する。
•隣接する辺のうち少なくとも2つは長さが等しい。菱形の面積は、平行四辺形と同じ方法で計算することができる。
平行四辺形と菱形の違いは何ですか?
•平行四辺形と菱形は四辺形です。菱形は平行四辺形の特殊なケースです。

•任意の面積は、ベースの高さの式を使用して計算できます。
•対角線を考慮する。平行四辺形の対角線は、お互いを二等分し、平行四辺形を二等分して2つの一致する三角形を形成する。菱形の対角線は互いに直交し、形成された三角形は等辺である。
•内角を考慮します。平行四辺形の対向する内角は同じである。 2つの隣接する内角が補足的である。菱形の内角は、対角線によって2等分される。






