限定的なものと不定のものとの間の差

として知られています。微積分は数学の重要な枝であり、微分は微積分において重要な役割を果たします。微分の逆過程は積分として知られており、逆は積分として知られているか、または単純に言えば、微分の逆数は積分を与える。彼らが生成する結果に基づいて、積分は2つのクラスに分けられる。 、明確な、そして不定の積分。

確定積分

<！ f（x）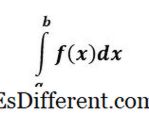

の定積分はNUMBERであり、 x = aから曲線999（x） 〜 x = b 999である。 積分には積分の上限と下限があり、問題の終わりには数があります - それは明確な答えです。 <！ （999）無限積分（999）f（x）の不定積分は関数であり、「微分するとどのような関数f（x） を与えるか」という質問に答える。 " 不定積分では積分に上限と下限はなく、まだ得られる答えは

x

であり、定数（通常は

C

で示される）を含む。 <！一般に、不定積分は、微分方程式に一般的な解を与える。 不定積分は、一般的な積分形式であり、考慮する関数の反微分として解釈することができます。関数f 999の微分が別の関数f 999をもたらし、fの積分が積分を与えると仮定する。象徴的には、これは、999および999の両方の場合に、F（x）=∫f（x）dx 999または999 F = は

x の関数であり、 F は微分可能である。上記の形式では、それはレイマン積分と呼ばれ、結果の関数は任意の定数を伴います。 不定積分はしばしば一連の関数を生成する。従って、積分は不定である。

積分と積分プロセスは、微分方程式を解くうえで中心的な役割を果たします。ただし、差別化の手順とは異なり、統合の手順は必ずしも明確で標準的な手順に従うとは限りません。時には、その解を基本関数の観点から明示することができないことがあります。その場合、解析解は、しばしば不定積分の形で与えられる。

微積分の基本定理

定理と不定積分は、微積分の基本定理によって以下のように結びついている：定積分

を計算するには、 不定積分 >（アンチ・デリバティブとしても知られている）を評価し、エンドポイント x = a および x = b

で評価する。

同じ関数の積分を評価すると、定積分と不定積分との間の差異は明らかになります。

次の積分を考えてみましょう。

OK。違いを見てみましょう。 統合のために、次の式につながる索引に1つを追加する必要があります。 この時点では C は単なる定数です。この問題には、 C の正確な値を決定するための追加情報が必要です。 その定式化された形で同じ積分を評価しよう。 e。上限と下限が含まれています。 【0214】図形的に言えば、我々は今、曲線999（y）= y 999 999とy 999 999 = 999との間の領域を計算している。 >。 この評価の最初のステップは、不定積分評価と同じです。唯一の違いは、今回は定数

C

を追加しないことです。

この場合の式は次のようになります。

これは次のようになります。 本質的には、式の中で3と2を代入し、その差を求めました。 これは以前の定数 C の使用とは対照的に、明確な値です。 一定の因子（不定積分に関して）をもう少し詳しく調べてみましょう。 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9しかしながら、多くの発現の差異であってもよく、そのうちのいくつかには、999,999,999,999,998,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999,999これは、操作中に定数が考慮されていないため、逆転が一意ではないことを意味する。したがって、一般に、9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9。ちなみに、Cは '積分定数' として知られています。 我々は次のように書く：

∫

3y

2

。 dx = y 999 + C 999 <！ - 1 - >

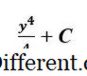
テーブルルックアップやRischの積分などの不定積分の積分手法は、積分プロセス中に新たな不連続性を追加する可能性があります。これらの新しい不連続点は、アンチデリバティブが複雑な対数の導入を必要とする可能性があるために表示されます。引数が負の実数軸を横切ると、複雑な対数はジャンプ不連続性を有し、時には積分アルゴリズムはこれらのジャンプがキャンセルされる表現を見つけることができない。 <！確定的積分が最初に不定積分を計算し、次に積分境界を結果に代入することによって確定積分が評価される場合、不定積分が不連続を生成する可能性があることに注意する必要があります。もしそうならば、積分区間の不連続性を調べなければなりません。